Assignments 33 - 37 - Computergrafik
Aufgabe 33
Aufgabe 34
Aus dem Skript folgt für das Drehen eines Punktes (X,Y) um den Ursprung um den Winkel b:
P(x’, y’) = P(x∙cos b - y∙sin b, x∙sin b + y∙cos b)
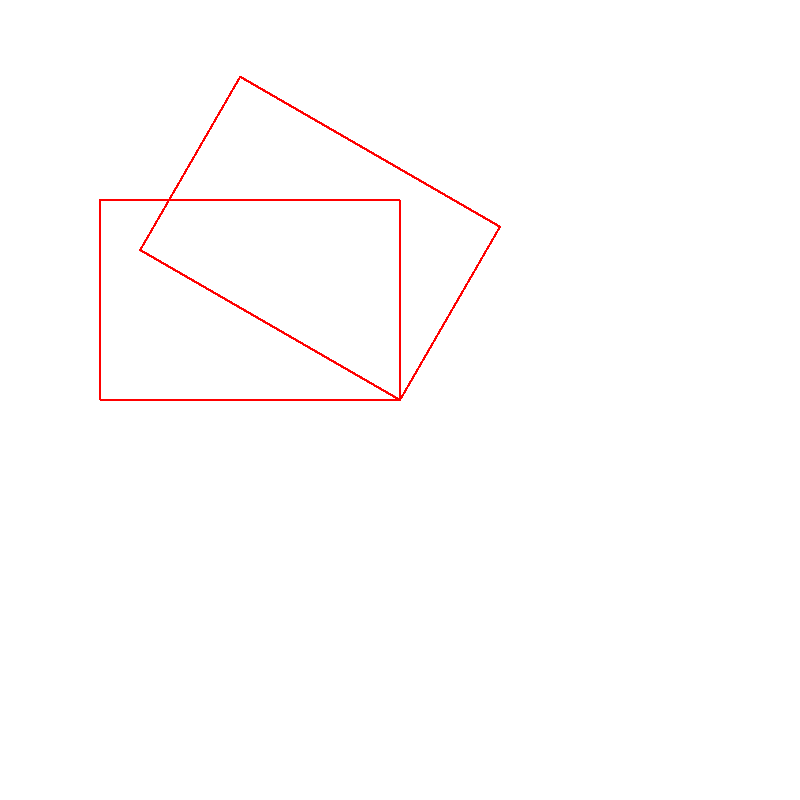
Das Viereck mit den Punkten (100,200), (400,200), (400,400) und (100,400) hat dann folgende Punkte wenn es um 10° um den Ursprung gedreht wird:
P1:
P(x’, y’) = P(100∙cos(10°) - 200∙sin(10°), 100∙sin(10°) + 200∙cos(10°))P(x’, y’)= P(63,75 , 214,33)
P2:
P(x’, y’) = P(400∙cos(10°) - 200∙sin(10°), 400∙sin(10°) + 200∙cos(10°))P(x’, y’)= P(359,19 , 266,42)
P3:
P(x’, y’) = P(400∙cos(10°) - 400∙sin(10°), 400∙sin(10°) + 400∙cos(10°))P(x’, y’)= P(324,46 , 463,38)
P4:
P(x’, y’) = P(100∙cos(10°) - 200∙sin(10°), 100∙sin(10°) + 200∙cos(10°))P(x’, y’)= P(29,02 , 411,29)
Diese Werte stimmen mit den Werten (64,214), (359,266), (325,463), (29,411) größtenteils überein. In diesem Fall dürfen wir die Rotationsformel für den Zweidimensionalen Raum auch für 3-Dimensionale Punkte verwenden, da der Dritte Wert immer 0 ist.
Aufgabe 35
Resultat:
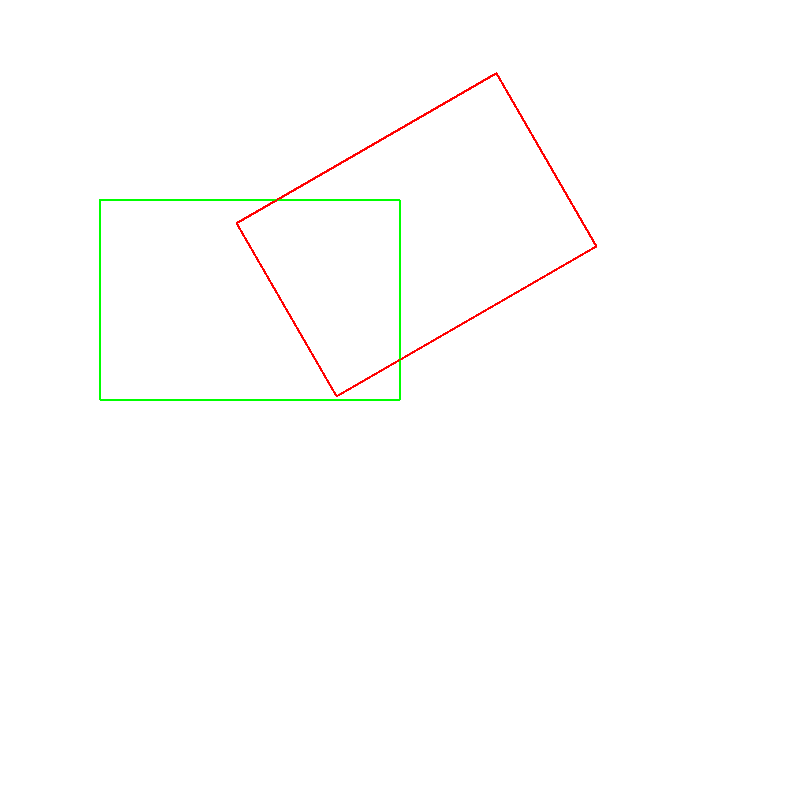
Aufgabe 36
Resultat:
Aufgabe 37

Die Textur in diesem Bild wir in der oberen Rechten und der unteren Linken ecke verzogen. Hierbei wird die Textur wie folgt verzogen:

Die Textur ähnelt also einem Trapez, da in den jeweiligen Ecken nicht die 0 punkte der Textur, sondern der Mittelpunkt angegeben wird. Deshalb erscheint die Textur so verzogen.